Toán Lớp 8: Ứng dụng của định lý Thalès và Tam giác đồng dạng

Trọng tâm của hình học lớp 8 là định lý Thalès và tam giác đồng dạng. Đồng thời đây cũng là một trong những dạng toán khó trong khối trung học cơ sở. Nhưng câu hỏi đặt ra là: Tại sao chúng ta phải cần biết các định lý này? Chúng giúp gì cho chúng ta trong cuộc sống hằng ngày? Chính vì thế bài viết ngày hôm nay sẽ phần nào giải đáp câu hỏi trên, và hi vọng sẽ giúp các bạn có hứng thú hơn khi làm các bài tập về dạng này.

Nhưng trước hết chúng ta phải điểm sơ qua các kiến thức cơ bản trước, sau đó mới có thể đi đến phần thực hành. Cụ thể cấu trúc của bài viết này như sau:

Định lý Thalès và định nghĩa tam giác đồng dạng;
Các ứng dụng trong cuộc sống;
Kết luận.

Định lý Thalès và định nghĩa tam giác đồng dạng

Định lý Thalès thuận

Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳngtương ứng tỉ lệ.

Với tam giác ABC, nếu có đường thẳng d song song với BC và cắt AB, AC lần lượt tại hai điểm D, E thì:

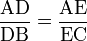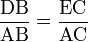$\frac{\mbox{AD}}{\mbox{AB}} = \frac{\mbox{AE}}{\mbox{AC}}$ và $\frac{\mbox{AD}}{\mbox{DB}} = \frac{\mbox{AE}}{\mbox{EC}}$ và $\frac{\mbox{DB}}{\mbox{AB}} = \frac{\mbox{EC}}{\mbox{AC}}$ .

Định lý Thalès đảo

Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

Với tam giác ABC, nếu có đường thẳng d cắt AB, AC lần lượt tại hai điểm D, E và:

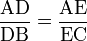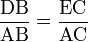
$\frac{\mbox{AD}}{\mbox{AB}} = \frac{\mbox{AE}}{\mbox{AC}}$ hay $\frac{\mbox{AD}}{\mbox{DB}} = \frac{\mbox{AE}}{\mbox{EC}}$ hay $\frac{\mbox{DB}}{\mbox{AB}} = \frac{\mbox{EC}}{\mbox{AC}}$

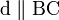thì $\mbox{DE} \parallel \mbox{BC}$ hay $\mbox{d} \parallel \mbox{BC}$ .

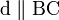Tam giác đồng dạng

Hai tam giác được gọi là đồng dạng nếu một trong chúng bằng với một tam giác nhận được từ tam giác kia sau một phép vị tự. Các điều kiện cần và đủ để hai tam giác đồng dạng:

Hai tam giác có các cặp cạnh tương ứng tỷ lệ thì đồng dạng.
Hai tam giác có hai cặp góc tương ứng bằng nhau thì đồng dạng.
Hai tam giác có hai cặp cạnh tương ứng tỷ lệ, góc xen giữa hai cặp cạnh ấy bằng nhau thì đồng dạng.

Các ứng dụng trong cuộc sống

Cách đo chiều cao Kim Tự Tháp Khufu của Thalès

Thalès là người đứng đầu trong bảy nhà hiền triết của Hy Lạp. Ông sống ở thành phố Milet khoảng thời gian từ năm 625 đến 547 trước Công nguyên. Ông tuy làm nghề buôn bán thời trẻ, nhưng ông lại có những công trình vĩ đại về toán học, thiên văn học, triết học, chính trị, khoa học tự nhiên. Vì thế ông được xem như là nhà toán đầu tiên của nhân loại. Nếu các bạn muốn tìm hiểu thêm, các bạn có thể vào wikipedia để có thêm chi tiết.nhé!

Một trong những giai thoại nổi tiếng là ông đã từng đo chiều cao của Kim Tự Tháp. Trước khi bạn đọc tiếp phần sau. Bạn hãy suy nghĩ thử xem ông đã thực hiện điều đó như thế nào nhé?

Giai thoại như sau: Thalès là một người rất được kính trọng thời đó, một hôm vua Ai Cập cổ đại đã mời ông vào triều vào nhờ ông một chuyện. Vua nói rằng:

Thalès, Ông biết đấy, Kim tự tháp Khufu là niềm kiêu hảnh của người dân Ai Cập chúng ta, nhưng mãi đến nay, không ai biết chiều cao chính xác của nó là bao nhiêu. Nếu ông có thể giúp được, người dân Ai Cập sẽ biết ơn ông rất nhiều.

Thalès nghe xong liền đồng ý, và ông nói ngày hôm sau sẽ tiến hành đo đạc ngay. Tin tức nhanh chóng lan truyền khắp nơi. Mọi người ai cũng tò mò để xem cách đo đạc như thế nào.

Khi đến hẹn, ông chỉ mang theo một cái cọc và một cấy thước. Một người rất thất vọng vì họ không tin rằng chỉ với dụng cụ đơn sơ như thế mà có thể đo được chiều cao của một Kim tự tháp khổng lồ như thế.

Một người bàn tán xôn xao, tuy nhiên ông vẫn thản nhiên, cắm cọc xuống đất như hình vẽ rồi lần lượt đo chiều cao của cái cọc, bóng của cái cọc và bóng của kim tự tháp. Như trong hình vẽ thì ông sẽ có số đo của x2, y2 và y1.

Từ kiến thức tam giác đồng dạng, ta có thể dễ dàng tính được x1 tức là chiều cao của Kim tự tháp như sau:

x1/x2=y1/y2

Rất hay phải không các bạn, và lưu ý với các bạn là thời đó chưa có kiến thức tam giác đồng dạng nên việc đo đạt như trên là nhờ sự thông minh của ông.

Lưu ý:

Việc đo đạc của Thales như thế nào, đến nay chưa biết rõ. Các làm như trên dựa theo Plutarch. Còn theo Hieronymus, một học trò của Aristote, thì cho rằng ông ghi lại chiều cao của Kim Tự Tháp vào thời điểm mà chiều dài của ông bằng chiều cao của ông (Tức là khi đó bóng của Kim tự tháp đúng bằng chiều cao của nó).
Người ta cũng không biết chính xác làm thế nào Thales có thể đo chính xác chiều dài của bóng. Như ta thấy, chiều dài của bóng phải tính từ tâm của Kim tự tháp.

Đo khoảng cách khi không thể tới được

Trong thực tế, chúng ta cần đo khoảng cách tới một vật nhưng lại không thể tới đó được do cách trở địa hình hoặc đến được nhưng không thể đo đạc được bằng thước. Sau đây là một ví dụ điển hình cho vấn đề này:

Hai ngôi nhà cách nhau 1 con sông, làm thế nào chúng ta có thể đo được khoảng cách 2 ngôi nhà đó. Hoặc phát biểu đơn giản hơn, tính chiều rộng của con sông.

Theo bạn, bạn sẽ làm như thế nào? Gợi ý nhé, tất nhiên là tam giác đồng dạng rồi. Để cho các bạn có thể giải trí, tôi sẽ không đưa lời giải (Bạn hãy nhìn hình dưới để biết cách giải nhé)

Các bạn nếu có lời giải thì comment ở phía dưới nhé.

Kết luận

Các bạn thấy đấy, điều tưởng chừng như bất khả thi hoặc trông rất khó khăn nhưng lại được giải quyết rất đơn giản từ những định lý của toán học phổ thông chúng ta.

Còn về phần các bạn, sau khi đọc xong bài viết này, tôi hy vọng các bạn sẽ thực hiện một số điều sau đây xem như bài tập về nhà:

Làm sao để biết được chiều dài chính xác của bóng Kim tự tháp.
Giải bài toán đo khoảng cách của con sông phần "Đo khoảng cách khi không thể tới được";
Hãy tìm thêm một số ví dụ ứng dụng tam giác đồng dạng trong thực tế cuộc sống nhé.

Nếu các bạn có thắc mắc hoặc có giải đáp được 3 vấn đề trên, vui lòng comment bên dưới để mình có thể rút thêm kinh nghiệm cho các bài khác nhé.

Cám ơn các bạn và hẹn gặp lại trong các bài viết khác!

Ứng dụng Toán học trong cuộc sống

Tìm kiếm Blog này